3 Points Make a Circle

While learning about Voronoi diagrams from Computational Geometry, I had trouble justifying a single statement from a proof regarding the complexity ( as a function of $n$ sites ) of Voronoi diagrams. For completeness I’ll restate the theorem here.

Theorem. For $n \geq 3$, the number of vertices in the Voronoi diagram of a set of $n$ point sites in the plane is at most $2n-5$ and the number of edges is at most $3n-6$.

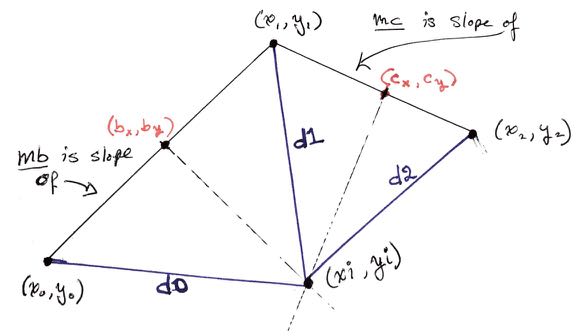
To establish the stated bounds, the proof hinges on the constancy of the Euler’s characteristic of graphs (that embed in $S^2$) and every vertex in the Voronoi diagram has degree at least three. Really? At the point in the proof when this fact is invoked we know that all the $n$ sites are not colinear; so given any pair of sites there’s a third site that does not lie on the line passing through them. Three points induce a vertex. But why?? Voronoi vertices have a specific meaning/interpretation; they are equidistant from sites, which means that a Voronoi vertex is the center of circle that passes through at least three sites.

Which, to me, begs the question: Is it always possible to find a circle that passes through three non-colinear points in the plane?

Well it’s true. Up to rotation and scaling the three given points can be positioned like so in the picture below.

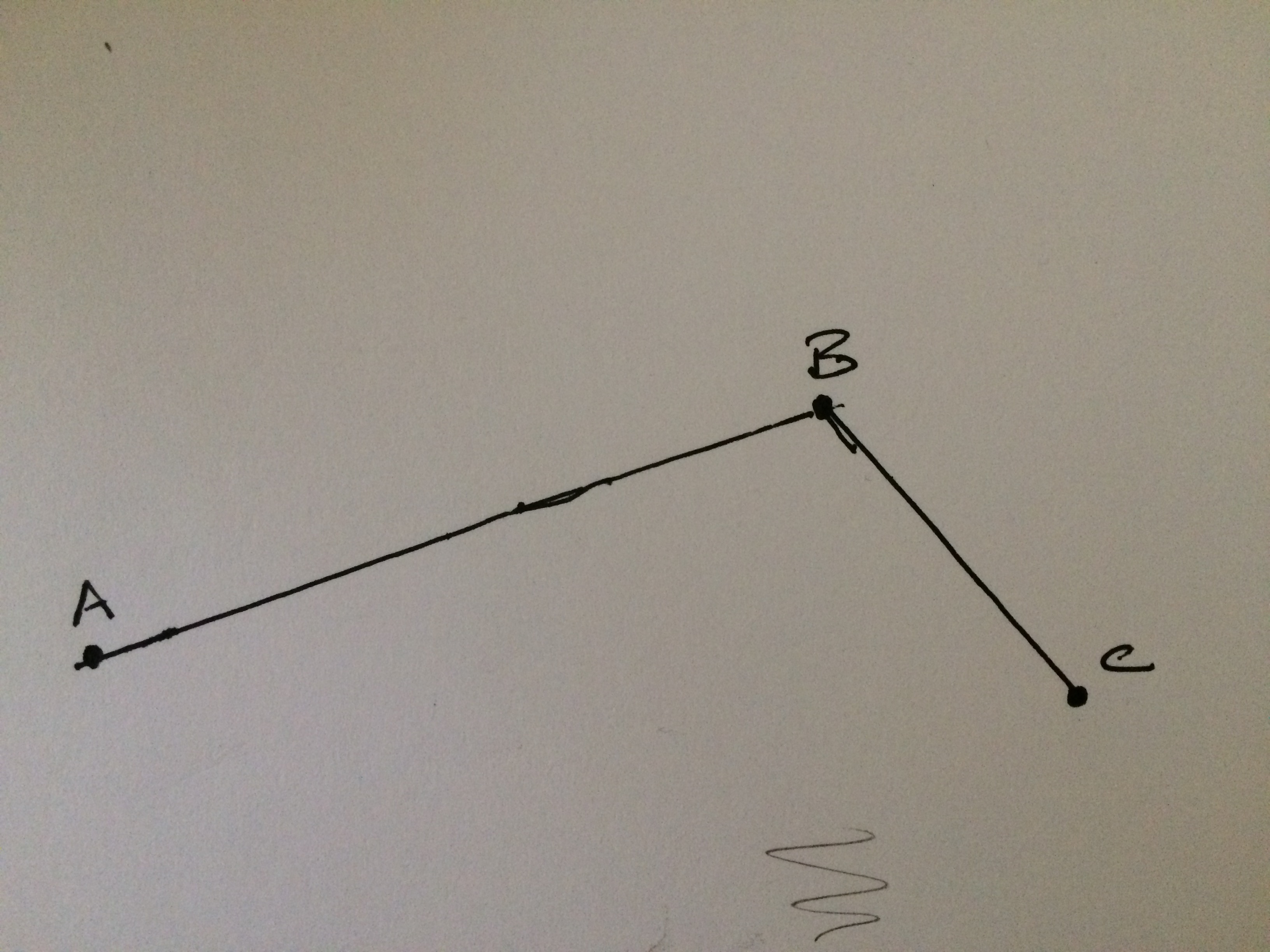
Edges $AB$ and $BC$ each have a line that bisects them; because the points form a proper triangle, these bisectors intersect.

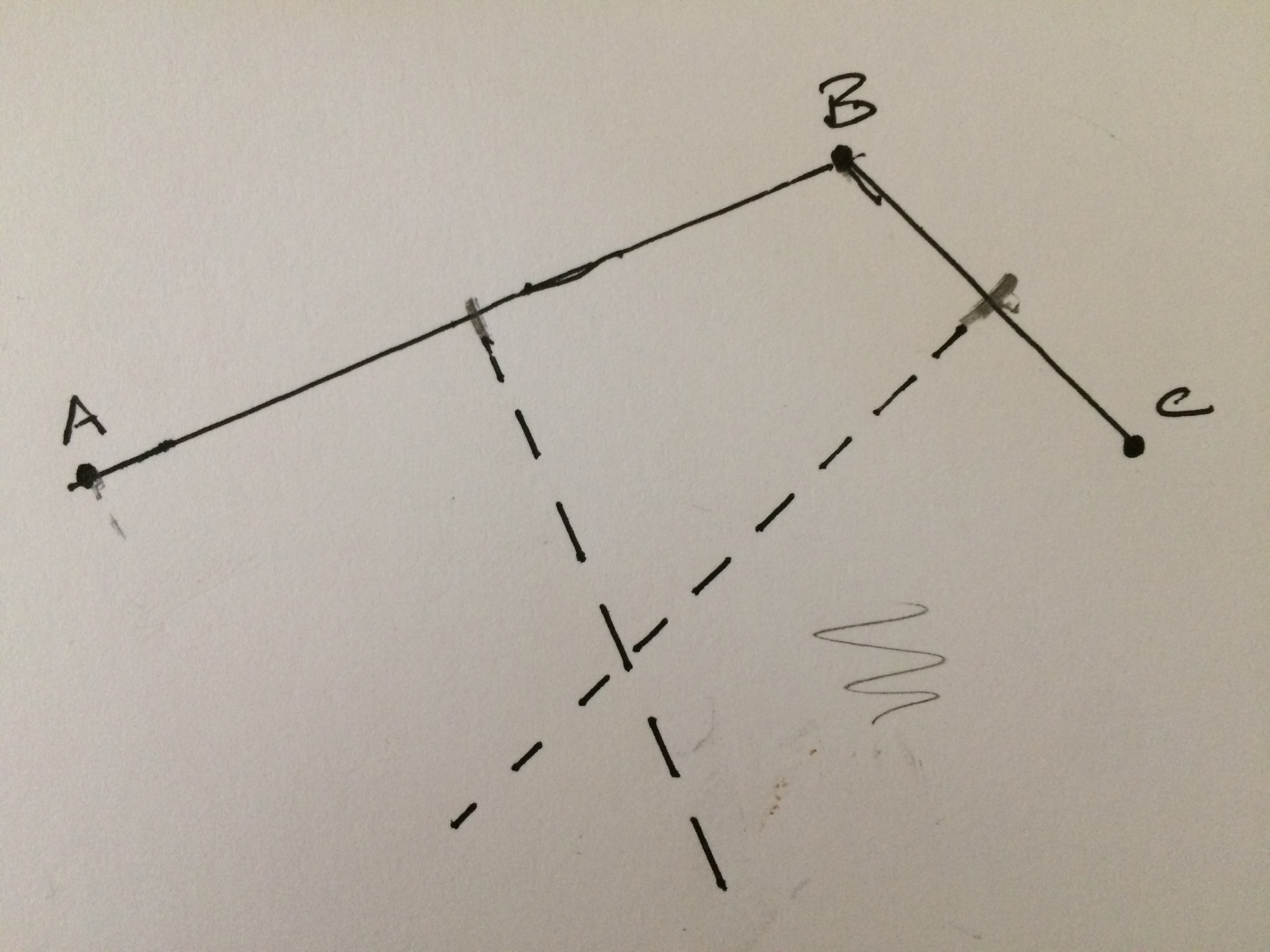
Voila! The intersection of the two bisectors is the center of a circle which passes through $A$, $B$, and $C$. The picture below shows the circle segment I constructed with a compass.

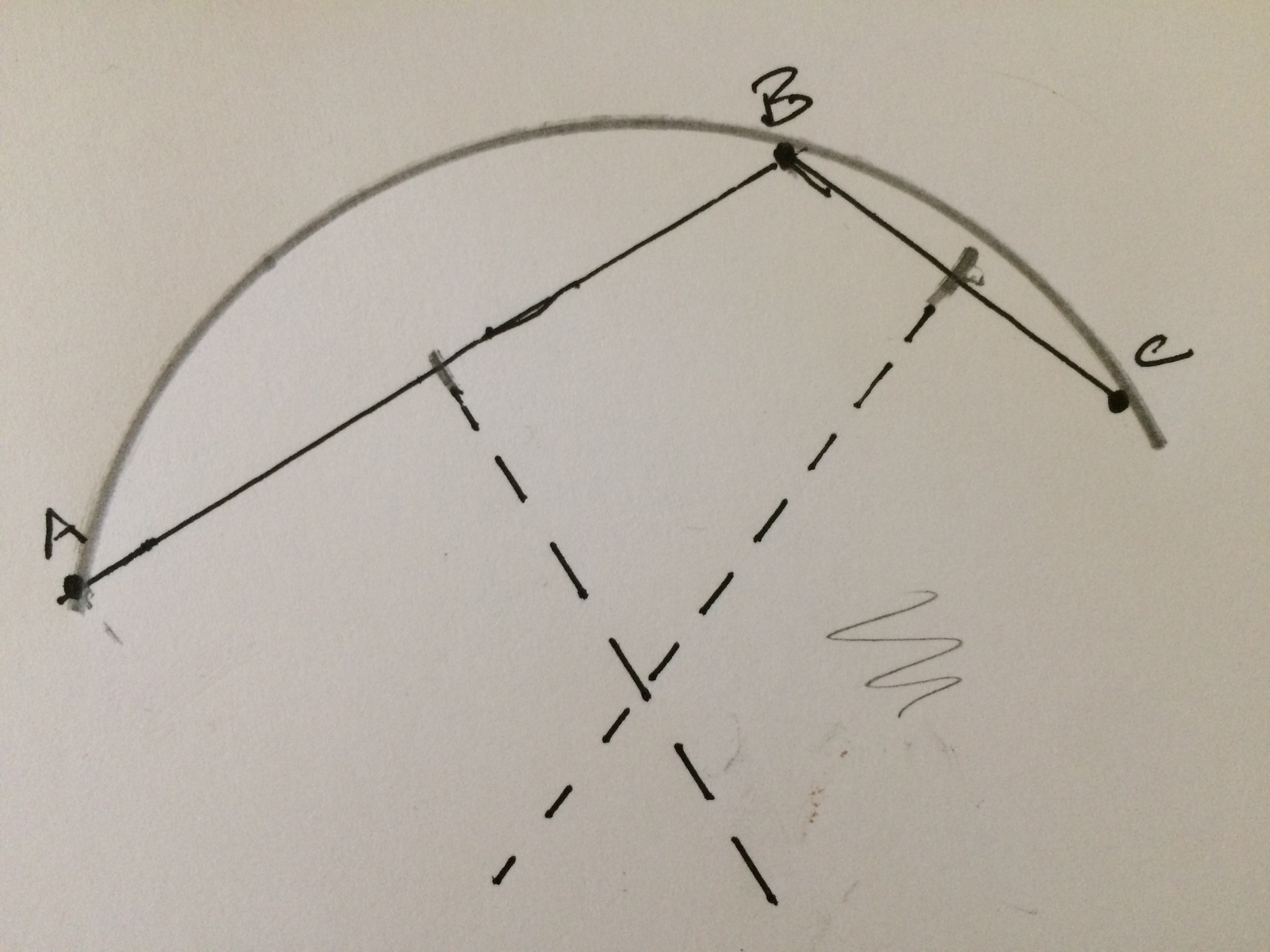
The circle segment above looks really good. Just a bit off the points $A$, $B$, and $C$; but all equally so. This is a proof by compass and ruler construction, and an elegant one at that. The alternative would be to compute the intersection of the bisectors in terms of coordinates and then verify a circle based there passes through all the points. As a check I did just that with the help of SymPy, a wonderful symbolic manipulation library. I drew Figure #4 below to help read the gist. When I ran the code, I showed, specifically, $d0 = d1 = d2$. Therefore, the circle of radius $d0$ passes through points $A$, $B$, and $C$.